Höhenkarten

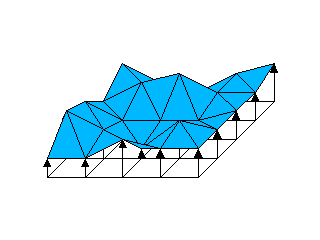
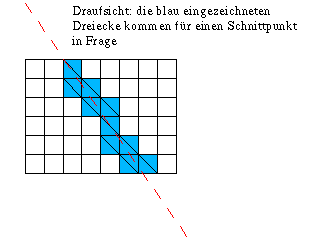
Höhenkarten sind - nach implizit definierten Oberflächen - die zweitkompliziertesten Objekte, was die Schnittpunktberechnung angeht. Man definiert sich ein Gitter aus m*n Punkten, und für jeden Gitterpunkt gibt man eine Höhe an. Die Gitterpunkte sollen nun mit Flächen verbunden werden, so dass keine Lücken entstehen. Sinnvollerweise nimmt man dazu Dreiecke, die man zwischen die Gitterpunkte legt (siehe Zeichnung). Jetzt könnte man auf die Idee kommen, gleich am Anfang einfach alle diese Dreiecke auszurechnen, um sie dann als normale Objekte zu behandeln. Allerdings: Gittergrößen von 2000x2000 sind nicht ungewöhnlich, und das wären 4 Millionen Dreiecke, also auch 4 Millionen Schnittpunkte pro Lichtstrahl! Und nicht nur das, der Speicherbedarf hierfür wäre immens groß! Also muss man sich einen Trick überlegen. Meiner geht so:
Nur ein Bruchteil aller dieser Dreiecke kommt überhaupt für einen Schnittpunkt in Frage, nämlich die, die von der Gerade "überflogen" werden, also die, die direkt über bzw. unter der Gerade liegen. Um diese herauszufinden, wird die Gerade zunächst auf die Gitterebene projiziert. Dann wird berechet, durch welche Gitterquadrate die Gerade verläuft; dazu benutze ich einen Linienalgorithmus, wie man ihn braucht, wenn man eine Gerade pixelweise auf den Bildschirm malen will. Für all diese Dreiecke wird nun temporär ein Dreieck-Objekt mit den entsprechenden Eckpunkten erzeugt und seine Schnittpunktprozedur aufgerufen.
Höhenkarten werden in meiner Implementierung so skaliert, dass sie in einen Standardwürfel hineinpassen.

Jetzt müssen nur noch die Gitterpunkte mit entsprechenden Höhenwerten belegt werden. Eine einfache Möglichkeit ist, dafür ein Bitmap zur Hilfe zu nehmen, und dabei die Summe aus Rot- Grün- und Blaukomponente als Höhenwert zu verwenden.

Um das Gitter mit Höhenwerten zu füllen, die wie eine fraktale Landschaft aussehen, benutze ich den Mittelpunktverschiebungsalgorithmus. Dabei wird jeweils der Mittelpunkt des Gitters um einen normalverteilten Zufallswert nach oben oder untern verschoben; dann wird das Gitter in vier Teile unterteilt, und mit diesen Teilen wird ebenso fortgefahren usw. . Dabei wird im Durchschnitt nach jedem Teilungsschritt weniger verschoben. Die so entstandene Landschaft ist ein Fraktal, dem man eine fraktale Dimension zuordnen kann; diese liegt zwischen zwei und drei. Je höher die fraktale Dimension, desto zerklüfteter ist die Landschaft. Bei dem Mittelpunktverschiebungsalgorithmus gibt man die fraktale Dimension vor, und abhängig davon wird berechnet, um wieviel im Durchschnitt in jedem Teilungsschnitt verschoben werden muss. Die genaue Beschreibung dieses Verfahrens findet man in dem Buch "Natur als fraktale Grafik" vom Markt&Technik-Verlag.

Eine weitere interessante Möglichkeit ist, die Höhenwerte aus einer benutzerdefinierten Funktion der Variablen x und y zu gewinnen. Was man dazu braucht, sind Routinen, die aus einem String, der die Funktion angibt, die Funktionswerte zu bestimmen. Meine Routinen machen folgende Schritte:
(1) Zerlege den String in eine Liste aus Einzelteilen (z.B. Operatoren, Funktion [sin,cos,..] usw.), mache dabei aus Dezimalzahlen double-Zahlen, finde Operatoren usw.
(2) Füge Klammern nach Punkt-vor-Strich hinzu
(3) Wandle die so erhaltene Liste in UPN (umgekehrte polnische Notation um), also z.B. sin(x+y) -> x y + sin
(4) Hier kann man jetzt leicht Werte für x und y einsetzen und die Funktionswerte ausrechnen.