 |
Torus, implizit definiert |
|
Einleitung
Implizit definierte Oberflächen sind die aufwändigsten Objekte und erscheinen auf den ersten Blick etwas abstrakt. Mit ihrer Hilfe kann
man aber einige sehr interessante Objekte konstruieren, wie z.B. Blobs ("Metaballs"), "Surface of Revolution", "Superquadric Ellipsoids".
Was man hier braucht ist Mathematik in Reinstform. Die einzelnen Algorithmen sind dabei teilweise etwas länglich; zu lang, um hier im
Detail vorgestellt zu werden. Ich werde daher nur das ungefähre Prinzip erläutern.
Eine implizit definierte Oberfläche, das ist eine Oberfläche, die durch eine Gleichung definiert ist. Punkte, die auf einer
Kugeloberfläche (Radius 1) liegen, erfüllen z.B. die Gleichung x^2+y^2+z^2=1 bzw. x^2+y^2+z^2-1=0. Damit ist die Kugel implizit definiert.
Allgemeiner: Ist f(x,y,z) eine Funktion der drei Koordinaten, dann möchte man die Oberfläche bestimmen, die aus denjenigen Punkte (x,y,z)
besteht, für die f(x,y,z)=0 ist. Ich habe das aber "nur" für den Fall implementiert, dass f(x,y,z) ein Polynom (beliebigen Grades) in den
drei Variablen x,y und z ist, damit kann man auch schon schöne Sachen machen.
[nach oben]
|
|
Auf der Suche nach Nullstellen
Zur Berechnung der Schnittpunkte muss man die Nullstellen von Polyomen beliebigen Grades in einer Variablen berechnen können. Für
Polynome zweiten Grades gibt es ja die bekannte p-q-Formel. Für Polynome dritten und vierten Grades gibt es zwar auch Formeln zur direkten
Berechnung der Nullstellen, die sind aber dann schon dermaßen kompliziert, dass sie durch Rundungsfehler schon leicht ungenau werden.
Daher benutze ich ab dem dritten Grad schon die allgemeine Methode. Ihr Funktionsprinzip ist etwa das folgende:
Zuerst kann man abschätzen, in welchem Intervall alle Nullstellen eines Polynoms liegen müssen. Dann bedient man sich der "Sturm´schen Ketten".
Diese Methode kann genau angeben, wie viele Nullstellen ein Polynom in einem bestimmten Intervall hat. Dafür muss man aber schon einige
Programmierarbeit leisten, denn man muss z.B. den ggT zweier Polynome berechnen können, und dafür braucht man den euklidischen Algorithmus, und
dafür braucht man Polynomdivision mit Rest usw..
Die Sturm´schen Ketten sagen also, wie viele Nullstellen in dem Intervall liegen. Liegen keine drin, ist man fertig. Wenn doch, dann kann
man das Intervall immer weiter halbieren, und mit jedem der Teilintervalle fortfahren. So kann man die Nullstellen beliebig genau bestimmen.
Der große Vorteil dieser Methode beim Raytracing ist, dass sie sehr exakt darin ist, anzugeben, ob ein Polynom eine Nullstelle hat oder nicht.
Der Ort der Nullstelle kann dann ruhig ein klein wenig ungenau sein.
[nach oben]
|
|
Schnittpunkt und Normalenvektor
Um den Schnittpunkt so einer Oberfläche mit einer Gerade zu berechnen, muss man sich zunächst die Geradengleichung in die drei
Komponenten (x,y und z) zerlegen und erhält dadurch drei Gleichungen von der Form x(t)=x0+t*dx; y(t)=y0+t*dy; z(t)=z0+t*dz. Diese
setzt man dann in die Oberflächenfunktion f ein und erhält ein Polynom f(t)=f(x(t),y(t),z(t)) in t. Von diesem muss man nun die Nullstellen
finden. Dazu benutzt man die oben kurz dargestellte Mothode. Gibt es keine Nullstelle, schneidet die Gerade das Objekt auch nicht. Wenn doch, dann halbiert man das
Intervall und fährt mit dem ersten Teilintervall fort, in dem eine Nullstelle liegt. Nach beliebig vielen Halbierungsschnitten hat man die
Nullstelle beliebig genau bestimmt. Die Methode der Sturm´schen Ketten hat den großen Vorteil, dass sie garantiert alle Nullstellen findet, was
für das Raytracing sehr viel wichtiger ist, als der genaue Ort der Nullstellen.
Nachdem man nun den ersten Schnittpunkt ermittelt hat, braucht man noch den Normalenvektor. Der ist der Gradient von f: v=grad f(x,y,z).
Das bedeutet: Die x-Komponente des Normalenvektors ist die Partielle Ableitung nach x von f an der Stelle des Schnittpunktes, ebenso berechnet
man y- und z-Komponente. Für Polynome kann man die partielle Ableitung nach einer Variablen glücklicherweise recht leicht ausrechnen.
Damit man dieses Objekt auch noch mit anderen Objekten kombinieren kann, braucht man noch die Berechnung, ob ein Punkt im Inneren des
Objektes liegt. Hier hat man es wieder etwas einfacher: Man muss den Punkt (x,y,z) nur in f(x,y,z) einsetzen; Ist das Ergebnis kleiner als 0,
so liegt der Punkt innen, sonst liegt er außen. Man muss dabei bei der Objektdefinition allerdings ggf. auf das Vorzeichen von f achten.
[nach oben]
|
 |
Superquadratischer Ellipsoid 6.Grades |
|
Anwendung: Superquadratische Ellipsoiden
Ein Superquadratischer Ellipsoid n. Grades ist eine Oberfläche, die durch die Gleichung x^n+y^n+z^n-1=0 definiert ist; dabei muss
n eine gerade Zahl sein. Man kann diese Definition auch für andere n "fortsetzen", aber das ist dann schon nicht mehr mit meinen Methoden
zu lösen. Ein Superquadratischer Ellipsoid 2. Grades ist eine Kugel.
[nach oben]
|
 |
Blob aus zwei Kugeln und einer Ebene |
|
Anwendung: Blobs, Typ I
Diesen erste Typ von "Blobs" hab ich mir selbst zusammengebastelt; man kann damit auch schon einige lustige Dinge machen. Gegenüber
den Metaballs (s.u.) haben sie aber den Nachteil, dass der Rechenaufwand mit der Komplexität des Objektes sehr stark ansteigt.
Meine Blobs sind so etwas wie Äquipotentialoberflächen. Dazu kann man drei verschiedene Potentiale addieren: Das erste ist Kugelsymmetrisch und
fällt mit dem Quadrat der Entfernung vom Mittelpunkt; das zweite ist Zylindersymmetrisch und fällt mit dem Quadrat des Abstandes von der
Zylinderachse; das dritte ist translationssymmetrisch (eben), es fällt mit dem Quadrat einer einzelnen Koordinate.
Diese drei Typen kann man nun beliebig kombinieren (addieren). Die Oberfläche des "Blobs" sind dann die Punkte, bei denen das Potential
einen bestimmten Wert annimmt.
Aufgabe ist es jetzt, aus dem Potential ein Polynom zu machen, auf das man oben beschriebene Methode anwenden kann. Dazu berechnet man
zunächst für die drei Potentialtypen den Kehrwert des Potentials. Beim Kugelpotential, dessen Zentrum in (x0,y0,z0) liegt, wäre das zum
Beispiel das Polynom (x-x0)^2+(y-y0)^2+(z-z0)^2. Bei den anderen beiden Typen ist das nicht ganz so einfach; Interessierte finden
aber in jeder guten Formelsammlung, wie man den Abstand Punkt-Gerade (für Zylinderpotentiale) bzw. Punkt-Ebene berechnet, den muss
man dann nur quadrieten. Auf diese Weise erhält man also Polynome pi(x,y,z). Das Gesamtpotential ist dann 1/p1(x,y,z)+1/p2(x,y,z)+...+1/pn(x,y,z).
Sucht man die Oberfläche, bei der das Potential den Wert I hat, muss man also die Gleichung
1/p1(x,y,z)+...+1/pn(x,y,z)=I
auf eine Form bringen, die man mit der oben genannten Methode lösen kann. Dazu multipliziert man beide Seiten der Gleichung mit dem "Hauptnenner"
und erhält
p2(x,y,z)*..*pn(x,y,z)+p1(x,y,z)*p3(x,y,z)*..*pn(x,y,z)+ ... +p1(x,y,z)*..*p(n-1)(x,y,z)=I*p1(x,y,z)*..*pn(x,y,z)
Dies kann man dann umformen zu
p2(x,y,z)*..*pn(x,y,z)+p1(x,y,z)*p3(x,y,z)*..*pn(x,y,z)+ ... +p1(x,y,z)*..*p(n-1)(x,y,z)-I*p1(x,y,z)*..*pn(x,y,z)=0
Damit ist das ganze auf die bekannte Form gebracht.
[nach oben]
|
 |
Metaball-Objekt aus drei Kugeln |

Die Wirkungsbereiche beim Metaball-Objekt
|
Anwendung: Blobs, Typ II (Metaballs)
Dies sind die Blobs (oft auch Metaballs genannt), wie sie auch in anderen Programmen implementiert sind. Mit viel Experimentieren
kann man damit ziemlich viel anstellen (siehe z.B. das "Krabbeltier" auf der Gallery-Seite). Ihr Aufbau ist ähnlich
wie bei den obigen Blobs: Man definiert Punkte (meine Metaballs unterstützen noch keine zylinder- oder flächenartigen Quellen), von denen
ein Potential der Form Intensität*(1-a^2/r^2)^2 ausgeht, wobei a der Abstand zum Punkt ist. r ist dann der "Radius" der Quelle.
Für Punkte außerhalb dieses Radius ist das Potential 0. Für das Gesamtobjekt werden wieder die einzelnen Potentiale addiert. Die Oberfläche
sind dann die Punkte, an denen das Gesamtpotential einen angegebenen Wert hat. Durch die abschnittsweise Definition (Potential =0 für Abstände
> r) kann man das gesamte Objekt aber nicht mehr geschlossen duch eine Oberflächengleichung darstellen. Vielmehr muss man den Raum in
Bereiche unterteilen, in denen jeweils bestimmte Punktquellen zum Potential beitragen. Die Bereiche werden also durch Kugeln begrenzt; Mehrere
Punktquelle wechselwirken nur da, wo sich diese Kugeln schneiden (siehe Abbildung links).
Für die Schnittpunktberechnung mit dem Lichtstrahl berechne ich zunächst alle Schnittpunkte mit diesen Bereichsbegrenzungskugeln. Für die
Teilbereiche (jetzt Streckenabschnitte auf dem Lichtstrahl) wird dann die Oberflächengleichung zusammengestellt (Addieren der Potentiale
aller beteiligten Punktquellen), mittels der man dann den Schnittpunkt kriegt. Hier kann man noch eine Optimierung anbringen: Wenn man einen
Bereich betrachtet, in dem nur eine einzige Punktquelle wirkt, dann kann man das Blob-Objekt durch eine Kugel mit entsprechendem Radius ersetzen.
[nach oben]
|
 |
Surface of Revolution |
|
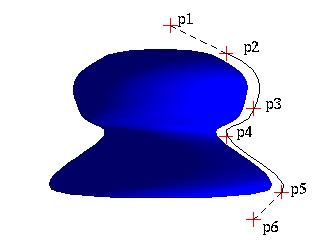
Anwendung: Surface of Revolution (SOR)
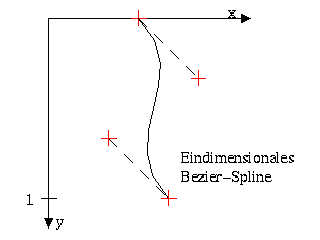
Bei "Surface of Revolution" handelt es sich um einen Rotationskörper, dessen Randkurve ein sogenanntes eindimensionales Bezier-Spline ist.
Ein Bezier-Spline verbindet Punkte so, dass fließende Übergänge entstehen. Der Kurvenzug wird dabei aus einzelnen Bezier-Splines zusammengesetzt,
die jeweils zwei Punkte verbinden. Zusätzlich zu diesen zwei Punkten gibt man für so ein Stück noch zwei Kontrollpunkte an (die mittleren
beiden in der Abbildung links), die den Kurvenverlauf bestimmen. Beim eindimensionalen Bezier-Spline hat (ohne Skalierung) der erste Punkt
die y-Koordinate 0, der letzte 1. Sind x1, x2, x3, x4 die x-Koordinaten der vier Kontrollpunkte, erhält man dann die Kurve durch
x=x1*i^3+3*x2*i^2*j+3*x3*i*j^2+x4*j^3, wobei i:=y und j:=1-y.
Nennt man obigen Ausdruck f(y), so erhält man dann die Oberflächengleichung durch x^2+z^2-f(y)^2=0, was ein Polynom 6. Grades ist.
Bei der Definition eines längeren Kurvenzugs aus diesen Splines nimmt der Raytracer einem zum Glück einen Teil der Arbeit ab, nämlich die
Kontrollpunkte zu definieren. Man muss nur die Punkte angeben, durch die die Kurve verlaufen soll. Der erste und letzte Punkt haben dabei
eine Sonderbedeutung: Durch sie wird die Kurve nicht verlaufen, sie geben nur an, mit welcher Steigung die Kurve beginnen und aufhören
sollen (siehe Abbildung).
[nach oben]
|
|
Copyright (c) 1999-2000 Martin Melcher
|



