Basisobjekte

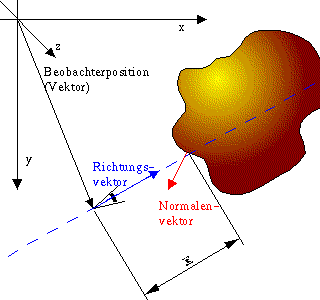
Beim Raytracing wird ein Objekt dadurch charakterisiert, wo seine Schnittpunkte mit Geraden liegen (siehe dazu auch Grundlagen), und in welche Richtung der Normalenvektor an diesen Schnittpunkten zeigt. Um ein Objekt zu definieren, muss man also eine Funktion schreiben, die zu einer vorgegebenen Gerade ermittelt, ob sie das Objekt schneidet, und in diesem Falle den ersten Schnittpunkt sowie den Normalenvektor an diesem Schnittpunkt berechnet. Wenn man später Objekte kombinieren will, braucht man zusätzlich eine Funktion, die ermittelt, welche Punkte innerhalb des Objektes liegen, und welche außerhalb.
Damit man sich nicht bei jedem einzelnen Objekttyp um Position, Verschiebung und Drehung kümmern muss, habe ich mir einen Trick ausgedacht: Vor der Schnittpunktberechnung wird die Gerade, mit der geschnitten wird, entsprechend verschoben, rotiert, und skaliert, dann erst die Schnittpunktprozedur des Objektes aufgerufen, und hinterher wird der Schnittpunkt und der Normalenvektor entsprechend zurücktransformiert. Auf diese Weise muss man sich bei der Implementierung eines neuen Objektes darum nicht mehr kümmern.
Die Schnittpunktprozedur des Objektes bekommt als Eingangsdaten eine Geradengleichung, diese ist geben durch den Richtungsvektor der Geraden, der auf die Länge eins normiert ist, sowie einen Punkt auf der Geraden (üblicherweise die Beobachterposition). Da der Schnittpunkt ja auf der Geraden liegt, muss nur der Abstand des Schnittpunktes von der Beobachterposition ausgerechnet werden. Dabei ist der Schnittpunkt zu berechnen, der den kleinsten positiven Abstand hat (ein negativer Abstand entspräche einem Schnittpunkt HINTER dem Beobachter).
Einige Objekte sind nur Kombinationen von anderen Objekten, so setzt sich z.B. ein Würfel aus seinen sechs Seitenflächen zusammen..

Die Kugel ist eines der einfachsten Objekte überhaupt. Den Schnittpunkt einer Kugel mit einer Geraden kann man durch relativ einfache Dreiecksberechnungen ausrechnen; Den Normalenvektor erhält man noch einfacher: Wenn da die Kugel im Koordinatenursprung ist und den Radius eins hat, ist der Normalenvektor gleich dem Schnittpunktvektor.

Das Quadrat braucht man eigentlich ausschließlich, um aus sechs davon einen Würfel zusammenzusetzen. Daher habe ich auch sechs verschiedene Quadrattypen implementiert, für jede Würfelseite eine. Für den Schnittpunkt braucht man zuerst den Schnittpunkt der Geraden mit der Ebene (xy-, xz- oder yz-Ebene), das ist die einfachste Schnittpunktberechnung überhaupt (Die Gerade schneidet die xy-Ebene da, wo ihre z-Koordinate 0 wird). Dann muss man noch überprüfen, ob der Schnittpunkt auf dem Quadrat liegt, dazu überprüft man, einfach, ob die einzelnen Komponenten kleiner als 0.5 sind (dann erhält man ein Quadrat der Kantenlänge 1).

Den Schnittpunkt mit einem Polygon zu berechnen, ist nur sinnvoll, wenn alle Punkte des Polygons auf einer Ebene liegen. Eine Ebene kann mathematisch dargestellt werden durch einen Punkt auf der Ebene (dazu wählt man einfach die erste Ecke des Polygons) und den Normalenvektor (den erhält man, wenn man das Kreuzprodukt der Vektoren bildet, die von der ersten Ecke auf die zweite und die letze Ecke zeigen). Wie man dann einen Schnittpunkt mit einer Geraden berechnet, steht eigentlich in jeder Formelsammlung. Was jetzt noch schwierig ist, ist die Überprüfung, ob der Punkt in dem Polygon drin liegt. Ich benutze dazu die Methode der Winkelsummen: Man berechnet die Winkel zwischen den Vektoren, die von dem Schnittpunkt auf je zwei benachbarte Ecken zeigen. Genau dann, wenn der Punkt im Polygon liegt, summieren sich die Winkel zu 360° bzw. 2 Pi. Das funktioniert aber auch nur bei konvexen Polygonen. Da diese Methode nicht besonders schnell ist, habe ich für Dreiecke eine andere Methode benutzt, die mir jemand aus der Newsgroup comp.graphics.algorithms gepostet hat. Das guckt man sich dann am besten im Quellcode an..

Hierbei handelt es sich um eine flache, runde Scheibe, mit einem runden Loch in der Mitte. Alleine braucht man die auch fast nie, aber man braucht sie später, um eine Röhre zusammenzusatzen. Für den Schnittpunkt braucht man zuerst wieder den Schnittpunkt mit der Ebene (die Scheibe liegt, wenn sie nicht rotiert wird, in der xz-Ebene). Dann muss man ausrechnen, ob der Punkt auf der Scheibe liegt; dazu muss man nur sehen, ob der Abstand vom Mittelpunkt zwischen den zwei Radien liegt. Man muss auf die Ausrichtung achten: Bei der "Standardscheibe" zeigt der Normalenvektor nach oben, die Rückseite wird, egal wie sie ausgerichtet ist, nicht beleuchtet.

Der "Standard"zylinder ist ein Zylinder mit dem Radius 1, der entlang der y-Achse von -1 bis +1 verläuft.
Die Formel für die Schnittpunktberechnung mit einem Zylinder habe ich mir mit einem Computeralgebraprogramm ausrechnen lassen. Dazu habe ich die Oberflächengleichung für einen Zylinder (x^2+z^2=1) eingegeben, für x und z die Komponenten der Geradengleichung eingegeben (x=x0+t*dx, z=z0+t*dz) und das Ganze nach t auflösen lassen.
Der Normalenvektor zeigt hier immer nach außen. Das gibt natürlich wieder ein Problem, wenn man in den Zylinder hineinsieht, denn wenn der Normalenvektor vom Beobachter weg zeigt, kriegt man keine vernünftige Beleuchtung. Im Allgemeinen ist es daher sinnvoller, eine Röhre zu benutzen, wo diese Probleme nicht auftreten.

Der Würfel setzt sich einfach aus sechs Quadraten zusammen. Der Standardwürfel hat die Kantenlänge eins.

Die Röhre besteht aus zwei Zylindern und zwei Scheiben. Bei der Schnittpunktberechnung muss man dann nur beachten, dass man die Richtung des Normalenvektors umkehrt, wenn der Schnittpunkt auf dem inneren Zylinder oder auf der unteren Scheibe liegt.

Die Schnittpunktberechnung für den Kreiskegelstumpf habe ich mir - genau wie beim Zylinder - von einem Computeralgebrasystem geben lassen, die sieht schon was gemeiner aus. Setzt man mehrere Kegelstümpfe zusammen, dann erhält man einen Rotationskörper. Auch hier muss man wieder mit der Richtung des Normalenvektors aufpassen, wenn man in das Objekt hineingucken kann.