
Grundlagen: Was ist Raytracing?
-> Beleuchtung
 |
Grundlagen: Was ist Raytracing? |
|
So funktioniert Raytracing -> Beleuchtung |
|
|
|
|
|
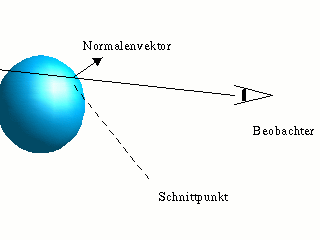
Was ist Raytracing? Raytracing - zu deutsch "Strahlen verfolgen" - ist ein Algorithmus, mit dem einigermaßen realistische Bilder erzeugt werden können. Die Idee dabei ist, den Strahlenverlauf zu simulieren, also unter Anwendung der physikalischen Gesetze (Brechungsgesetz etc.) den Weg der Lichtstrahlen zu berechnen. Allerdings geschieht dies "rückwärts": Man gibt vor, aus welcher Richtung ein Lichtstrahl in das Auge des Betrachters (die Kamera) fällt (abhängig von den Koordinaten des zu berechnenden Punktes im fertigen Bild), und ermittelt seine Vergangenheit, also wo er herkommt. [nach oben]Die Berechnung Da sich das Licht bekannterweise nur geradlinig ausbreitet, liegen alle Punkte, die den Lichtstrahl ausgesendet haben könnten, auf einer Geraden, deren Gleichung aus der vorgegebenen Richtung hervorgeht. Als einzige Quellen kommen aber nur die Objekte in Frage (da es im idealisierten Fall nur punktförmige Lichtquellen gibt, existiert der Fall, dass man direkt in eine Lichtquelle sieht, nicht). Und nun kommt der zentrale Punkt im Raytracing: Man muss berechnen, wo die Gerade die einzelnen Objekte schneidet. Interessant ist natürlich zunächst nur der Schnittpunkt, der am nächsten liegt. Nun kommt der zweite wichtige Punkt: Welche Farbe und Helligkeit hat der Lichtstrahl denn nun? Dazu muss man die Ausrichtung der Objektoberfläche kennen. Dazu benutzt man ein mathematisches Hilfsmittel, den "Normalenvektor", der an jedem Punkt senkrecht auf einer Oberfläche steht. Diesen muss man für den gefundenen Schnittpunkt ermitteln. Danach kann man den Winkel zur Geraden und zu den Lichtquellen, sowie den Abstand zur Lichtquelle berechnen. Je nach Oberfläche ergibt sich die Helligkeit. Nun ist man aber noch nicht fertig: Das Objekt könnte verspiegelt oder gar durchsichtig sein! Es könnte also sein, dass ein Anteil des Lichtes von reflektierten oder von hinter dem Objekt kommenden Lichtstrahlen herrührt. Da aber der Normalenvektor der Oberfläche und Materialeigenschaften des Objektes bekannt sind, kann man berechnen, aus welcher Richtung diese Lichtstrahlen kommen müßten. Also nimmt man diese Richtungen nun als neue Geradengleichung und fängt das ganze Spiel von vorne an. Im Prinzip ist Raytracing also eine rekursive Sache. [nach oben] |
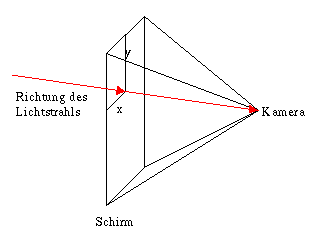 |
Die Kameraprojektion
Zu allererst braucht man erst einmal die Richung des Lichtstrahls, den man zurückverfolgen möchte, und die muss man sich abhängig von Kameraposition, -ausrichtung, Bildauflösung und Koordinaten des Punktes, den man gerade betrachtet, ausrechnen. Dazu denkt man sich einen Schirm, auf den das Bild projiziert wird. Dann muss man die Vektoren der vier Eckpunkte des Schirmes ausrechnen, und kann dann dazwischen linear interpolieren [nach oben] |
|
Schnittpunktberechnung
Hat man sich so die Richtung des Lichtstrahls ausgerechnet (den Ursprung kennt man ja, das ist die Kameraposition), berechnet man alle Schnittpunkte dieses Lichtstrahls mit allen Objekten. Um die Berücksichtung der Position und Lage im Raum sowie die Größe der Objekte einfacher zu machen, wird dabei der Lichtstrahl entsprechend umgekehrt verschoben, skaliert und gedreht. Auf diese Weise kann man später bei der Schnittpunktberechnung davon ausgehen, dass das Objekt im Koordinatenursprung liegt, Einheitsgröße hat, und entlang der Koordinatenachsen ausgerichtet ist. [nach oben] | |
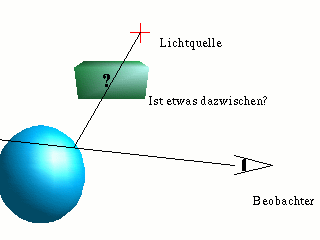 |
Licht und Schatten
Als nächstes muss bestimmt werden, von welchen Lichtquellen aus Licht auf den gerade gefundenen Punkt fällt. Dazu wird für jede Lichtquelle die Gerade bestimmt, die durch den Schnittpunkt und die Lichtquelle geht (dabei werden Lichtquellen als punktförmig angenommen). Anschließend werden alle Schnittpunkte dieser Gerade mit allen Objekten berechnet; gibt es einen, der zwischen Objekt und Lichtquelle liegt, fällt kein Licht auf den Punkt (er ist im Schatten). Es kann aber auch sein, dass das schattenspendende Objekt transparent ist; dann muss die Lichtfarbe und -Intensität entsprechend geändert werden. Mit den ensprechenden Beleuchtungsmodellen und den definierten Oberflächeneigenschaften des Objektes kann jetzt die Farbe des Pixels berechnet werden. [nach oben] |
|
Die Rekursion
Bis jetzt kennt man also den Lichtanteil, den das Objekt direkt von den Lichtquellen reflektiert. Nun könnte es aber auch verspiegelt
der durchsichtig oder gar beides sein. Wenn es verspiegelt ist, dann muss man zuerst den Richtungsvektor zum Beobachter am Normalenvektor
spiegeln und seine Richtung umkehren. Was man erhält, ist die Richtung, aus der das Licht kommen muss, um in Beobachterrichtung reflektiert
zu werden. Dann muss man die Farbe dieses Lichtes berechnen; dazu geht das ganze Spiel von vorne los, nur dass man jetzt anstatt von der
Beobachterposition von dem Punkt ausgeht, an dem das Licht reflektiert wird. Die Raytracingfunktion muss sich dann also selbst nochmal
aufrufen. Damit die Berechnung aber irgendwann fertig ist, ist es sinnvoll, eine maximale Rekursionstiefe zu definieren, nach der die
Rekursion abbricht. Hat man jetzt also die Farbe des Lichtes, das reflektiert wird, muss man sie noch mit der Objektfarbe kombinieren (denn
z.B. wirft ein rotes Objekt ja nur den Rotanteil zurück), also die beiden Farben multiplizieren. | |